Lab 8 - More Functions with Turtle Graphics
Directions for Labs
- Submit your completed lab file online to CourSys (not Canvas). Labs are marked on completion, not correctness, so complete each part to the best of your ability and learn!
- It is recommended that students attend in-person lab sections for lots of help!
- If you would like to attend an in-person lab section, you are welcome to come to any (or more than one) lab section.
- There is no need to attend the section you are enrolled in.
- There is no need to attend any lab sections: there is no attendance taken.
- You can complete the lab on your own time or own computer if you like.
- While completing these labs, you are encouraged to help your classmates and receive as much help as you like. Assignments, however, are individual work and you must not work with another person on assignments.
Part 1) Print factors
- Inside your
cmpt120folder, create a new folder forlab8and make alab8.pyfile.- See lab 1 for more detailed directions.
- Create a fruitful function which asks the user to enter a number (an integer) between 1 and 20 inclusive.
- If the user enters a value less than 1, or greater than 20, print an error message and have the user enter a new value.
- Once the user enters a valid integer, return the value.
- In your calling "main" code, call your function and store the value in a variable named
num. - For now, just print
numin your calling code (we'll use it in the next steps). -
Hint - return and receive:
Your function must return the value the user entered, and your calling code must store the return value into a variable. -
Hint - No print:
Your function should not print the number the user entered: we'll have the calling code print it for the moment. -
Hint - While:
Ues awhileloop in your function to ensure the user's input is valid. - Sample output:
Enter a number: -1 Number must be between 1 and 20 Enter a number: 22 Number must be between 1 and 20 Enter a number: 16
- Create a fruitful function named
is_divisible(...)which accepts two integer arguments namenumanddiv.- Return
Trueifnumcan be evenly divided bydiv. Otherwise, returnFalse. -
Hint - mod:
Remember that you can check if A is divisible by B with:if A % B == 0:... -
Hint - Code:
Here is some code that works (but can be improved! See next 2 hints):def is_divisible(num, div): if num % div == 0: return True else: return False -
Hint - no if:
Rather than using an if statement, you can just return the Boolean expression. -
Improvement - Better Code:
Here is some better code. It just uses the expression directly and saves us some logic. Any time your if statement just returns True/False, you likely want to do this:def is_divisible(num, div): return num % div == 0
- Return
- In the "main" code, create a loop to print out which integers between 1 and
num(inclusive) divide evenly intonum(i.e., for whichis_divisible()is True)-
Hint - for range:
Create a for loop in the "Main" area (outside of any function) which has a range ofrange(1, num + 1) -
Hint - code:
The full code in the "main" area may look like:num = read_number() for i in range(1, num + 1): print(f"Is {i:2} a factor of {num:2}? {is_divisible(num, i):2}") - Sample output:
Enter a number: 12 Is 1 a factor of 12? 1 Is 2 a factor of 12? 1 Is 3 a factor of 12? 1 Is 4 a factor of 12? 1 Is 5 a factor of 12? 0 Is 6 a factor of 12? 1 Is 7 a factor of 12? 0 Is 8 a factor of 12? 0 Is 9 a factor of 12? 0 Is 10 a factor of 12? 0 Is 11 a factor of 12? 0 Is 12 a factor of 12? 1
-
- Print only the factors of
num.- Change your calling code's loop to only print the factors of
num, rather than printing all numbers between 1 andnum. -
Hint - if:
use an if statement such as:if is_divisible(num, i): print(f"Factor: {i}")
- Change your calling code's loop to only print the factors of
Part 2) Draw Factors
- Add the necessary code to do turtle graphics
- This includes the import, declaring your turtle, and likely holding the window open until click.
- You may want to speed up the drawing with:
picasso.speed(0)
- Create a function to draw a rectangle.
- Pass in (arguments) a the location of the lower-left corner:
x,y. - Also pass in (arguments) the
widthandheightof the rectangle. - Use turtle graphics to draw the rectangle up and to the right of the lower left corner (
x,y). -
Hint - Function:
1st line of function definition might be:def draw_rectangle(x, y, width, height): -
Hint - Turtle:
Use the turtle .penup(), .pendown(), and .goto(...) functions to move around and control drawing. Or, instead of using goto(...) you can also draw with the pen down by turning the turtle and moving forward.
- Pass in (arguments) a the location of the lower-left corner:
- Draw a rectangle for each factor.
- For each factor
hcomputewsuch thath * w == num. For example, ifnumis 12 andhis3, thenwwould be4. - Draw a rectangle starting at (0,0) with height
h * 30and widthw * 30. - For example, for
num= 5 there will be two boxes. One for 5x1 and the other for 1x5. Each dimension is multiplied by 30 pixels so the two boxes will have height and width of 150x30 and 30x150 pixels. -
Hint - Integer Division:
For allhwhereis_divisible(num, h)is true, height ish * 30; width is(num // h) * 30 - Example (OK to end up with the turtle in any position).
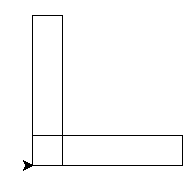
- For each factor
- Create a function named
draw_message(...)which writes some text at location (x,y).- Pass in (argument) the x and y locations, plus a message.
- Move to that location and then use
my_turtle.write(message) - Remember to use
penup()andpendown()as needed. -
Hint - Function Definition:
Use the following 1st line of the function:def draw_message(x, y, message):
- Add messages to your drawing
- For each factor rectangle, write beside it the numbers for its size. For example, with
num= 10, you'll have boxes labeled "1x10", "2x5", "5x2", and "10x1". OK to have numbers in opposite order. Labels may be placed anywhere on the rectangles that it is clear. - For the entire graph, write "
Factors of {num}" using yourdraw_message(...). - Sample output with labels
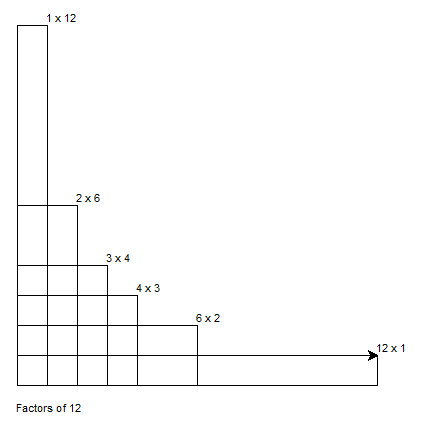
- For each factor rectangle, write beside it the numbers for its size. For example, with
- Refactor your code to put the calling code from the "main" area into is own function.
- Suggested function
draw_factors(num) - Your code in the "main" area should look like:
num = read_number() draw_factors(num)
- Suggested function
Part 3) Draw a Parabolic Curve
- We will be drawing the following figure.
- For the basic idea, see this guide to drawing parabolic curves with straight lines (method 1).
- You can do this on your own, or read on for the step-by-step guide.
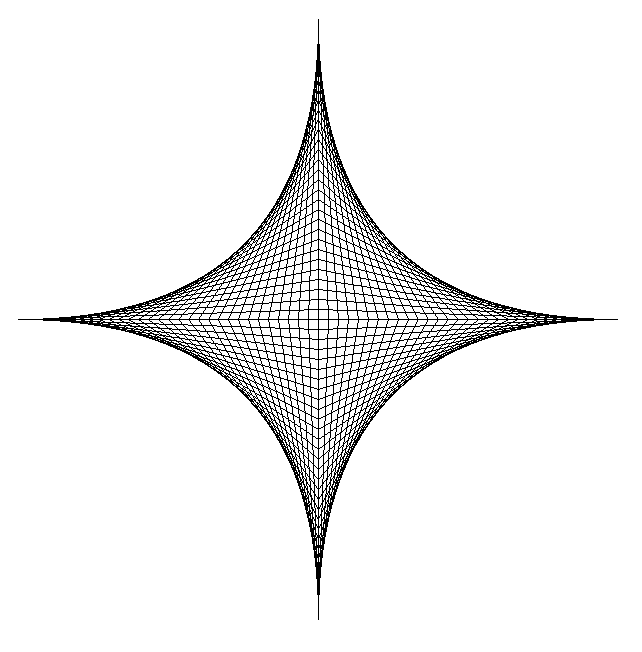
- Comment out the calls to the above code.
- In the "main" area, loop through lines:
- Setup a variable named
SIZEto be 300. - Setup a loop going from 0 to the
SIZE(inclusive) in steps of 10. Name the variableoffset
- Setup a variable named
- In the loop, draw the lines for the top half of the figure:
-
Hint - use goto(x,y):
When you know the coordinates, it's easiest to usemy_turtle.goto(x, y)rather than trying to move forwards/backwards and turning. -
Hint - Left:
Start on the left at position(-SIZE + offset, 0); usemy_turtle.goto(x,y). -
Hint - Middle:
Move to the middle point at position(0, offset). -
Hint - Right:
Move to the right point at position(SIZE - offset, 0) -
Hint - Pen up/down:
Put the pen up before moving to the starting position without drawing. Put the pen down to start drawing when doing goto(...) operations. - Test your code: you should see the top half of the figure.
-
- Do the same for the bottom lines.
- Move your code to draw the shape into a well named function.
- Now pass in an (x,y) parameter to the function so you can draw your shape on the screen in a different location.
- Remember to add +x and +y as needed to where the turtle will move.
- Have your code draw a total of two of these shapes.
- Optional: Convert your code which draws the parabolic curved shape to use a
whileloop over aforloop.- A
forloop is easier for this situation; however, it's possible to use awhileloop. Give it a try.
- A
Submission
Uncomment all your code before submitting.
Submit your lab8.py file to CourSys by Sunday midnight. Remember you can submit up to 3 days late with no penalty if needed (but please plan to get it done on time to stay up to date on the course!)
Topics Covered
- Designing with functions
- DRYing out code using functions
- Functions calling functions
- Fruitful functions
- While loop
- Draw the + straight line figure